Answer: The required distance is given by
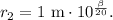
Explanation: The sound intensity in dB is given by the formula
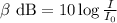
where
 is the hearing threshold in absolute units and
is the hearing threshold in absolute units and
 is the absolute intensity of the sound which depends on the distance. In general, for two distances
is the absolute intensity of the sound which depends on the distance. In general, for two distances
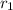 and
and
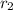 we have that
we have that
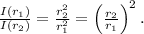
Now let us take
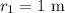 and let
and let
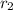 be the required distance. We have
be the required distance. We have
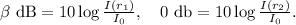
Exponentiating these equations we obtain
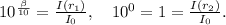
Dividing them
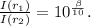
Using the previously stated identity
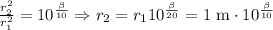
Now if we use the given example where
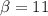 we have
we have
