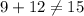Question

The areas of the squares created by the side lengths of the triangle are shown. Which best explains whether this triangle is a right triangle? 9sqrt 12sqrt 15sqrt

Answer 1

B

Explanation:

Answer 2

Based on the converse of the Pythagorean Theorem, the triangle is not a right triangle, because
`9+12\\eq 15`

Explanation:

The complete question in the attached figure

we know that

If the length sides of a triangle, satisfy the Pythagorean Theorem, then is a right triangle

`c^2=a^2+b^2`

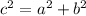
where

c is the hypotenuse (the greater side)

a and b are the legs

In this problem

The length sides squared of the triangle are equal to the areas of the squares

so

`c^2=15\ in^2`

`a^2=12\ in^2`

`b^2=9\ in^2`

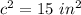
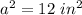
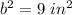
substitute

`15=12+9`

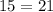`15=21` ----> is not true

so

The length sides not satisfy the Pythagorean Theorem

therefore

Based on the converse of the Pythagorean Theorem, the triangle is not a right triangle, because
`9+12\\eq 15`