Question

Engineers can determine properties of a structure that is modeled as a damped spring oscillator, such as a bridge, by applying a driving force to it. A weakly damped spring oscillator of mass 0.206 kg is driven by a sinusoidal force at the oscillator's resonance frequency of 33.8 Hz. Find the value of the spring constant.

Answer 1

Spring Constant K=9290.9550 N/m

Step-by-step explanation:

Formula we are going to use is:

`2\pi f=\sqrt{(K)/(m)}`

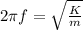
Where:

f is the frequency

K is the spring constant

m is the mass

Given:

Mass of spring oscillator=m=0.206 kg

Resonance Frequency=f=33.8 Hz

Find:

Spring Constant=K=?

Solution:

From Above formula:

Taking Square on both sides

`4(\pi)^2f^2=(K)/(m) \\K=4(\pi)^2f^2*m\\K=4(\pi)^2(33.8)^2*(0.206)\\K=9290.9550 N/m`

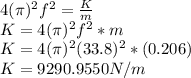
Spring Constant K=9290.9550 N/m