Question

A red train traveling at 72 km/h and a green train traveling at 144 km/h are headed toward each other along a straight, level track. When they are 920 m apart, each engineer sees the other's train and applies the brakes. The brakes slow each train at the rate of 1.0 m/s2. Is there a collision? If so, give (a) the speed of the red train, (b) the speed of the green train, and (c) the separation between the trains when they collide (0 m). If not, give (a) the speed of the red train (0 m/s), (b) the speed of the green train (0 m/s), and (c) the separation between the trains when they stop.

Answer 1

1. they would collide.

2. 0 m/s

3. v = 12.65 m/s

4. 0 m

Step-by-step explanation:

speed of red train (u1) = 72 km/h = 20 m/s

speed of green train (u1) = 144 km/h = 40 m/s

distance of trains apart (d) = 920 m

acceleration (a) = - 1 m/s^{2} (negative sign is because the train is decelerating)

1. To find out if the trains collide, we can get the distance at which they would both stop and add the up to see if it would be more than 920 m

`v^(2) = u^(2) + 2as`

s =
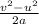`(v^(2)-u^(2) )/(2a)` where v is the final velocity and is = 0, and inserting all

required values into the equation we have:

distance the red train stops at (s) =
`(0^(2)-20^(2) )/(2x(-1))` = 200 m

distance the green train stops at (s1) =
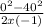`(0^(2)-40^(2) )/(2x(-1))` = 800 m

total distance = 800 + 200 = 1000 m

1000 m is greater than the distance between the trains (920 m), hence they would collide.

2. From the calculation above, the red train stops before they collide since it was travelling at a lower velocity. We can get the time it takes for the red train to stop and use that time to get the distance the green train would have reached so as to confirm that the red train will have come to a rest before the collision by adding the distance the green train would have covered to the distance the red train stops at (200 m)

from v = u + at

t = (v-u)/a

time it takes for the red train to stop (t) = (0-20) /(-1) = 20 s

In 20 s the green train would be at:

s = ut + 0.5a
`t^(2)`

s = 40(20) - (0.5 x (-1) x (20x20))

s = 600 m

adding the distance the red train stops at (200 m) to the distance the green train covers (600 m) under the same time interval we have

200 + 600 = 900 m which is less than the distance between the two trains.

Hence the red train would have stopped before the trains collide and would be at 0 m/s

3. The green train hits the red train at 920 - 200 = 720 m, hence the final velocity of the green train can be gotten from

`v^(2) = u^(2) + 2as`

`v^(2) = 40^(2) + (2x(-1)x720)`

`v = \sqrt{40^(2) + (2x(-1)x720)}`

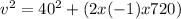
v = 12.65 m/s

4. Since both trains collide, they would be no separation between the trains. Hence the separation = 0 m