Answer:
The minimum value for
 is
is
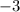 .
.
Explanation:
Given function is

We need to find the maximum value or the minimum value for the function.
Now, differentiate
 w.r.t
w.r.t
 .
.


Now, we will equate
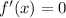 to find critical point.
to find critical point.
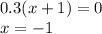
Plug this critical point in to the function
 we get,
we get,
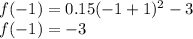
Also,
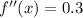 which is positive, We have minimum value.
which is positive, We have minimum value.
So, the minimum value for
 is
is
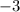 .
.