Answer :
The least possible uncertainty in an electron's velocity is,
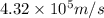
The percentage of the average speed is, 33 %
Explanation :
According to the Heisenberg's uncertainty principle,
 ...........(1)
...........(1)
where,
 = uncertainty in position
= uncertainty in position
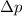 = uncertainty in momentum
= uncertainty in momentum
h = Planck's constant
And as we know that the momentum is the product of mass and velocity of an object.
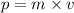
or,
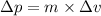 .......(2)
.......(2)
Equating 1 and 2, we get:
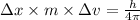
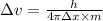
Given:
m = mass of electron =
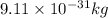
h = Planck's constant =
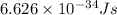
radius of atom =
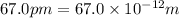
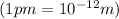
 = diameter of atom =
= diameter of atom =
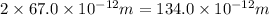
Now put all the given values in the above formula, we get:
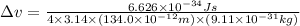
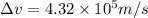
The minimum uncertainty in an electron's velocity is,
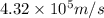
Now we have to calculate the percentage of the average speed.
Percentage of average speed =

Uncertainty in speed =
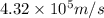
Average speed =
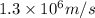
Percentage of average speed =
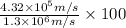
Percentage of average speed = 33.2 % ≈ 33 %
Thus, the percentage of the average speed is, 33 %