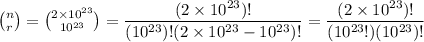Answer:
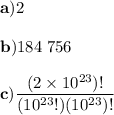
Explanation:
If the system contains
 atoms, we can arrange
atoms, we can arrange
 quanta of energy in
quanta of energy in
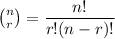
ways.
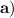
In this case,
 .
.
Therefore,
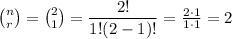
which means that we can arrange 1 quanta of energy in 2 ways.

In this case,
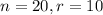 .
.
Therefore,

which means that we can arrange 10 quanta of energy in 184 756 ways.
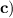
In this case,
 .
.
Therefore, we obtain that the number of ways is