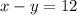Question

Find an equation for the line in the form of ax+by=c where a,b,c are interferes with no common to all three and a. Through (3,-9), perpendicular to x+y=6

Answer 1

The equation for the line in the form of
`ax+by=c` is
`x-y=12`

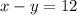
Explanation:

Given point is
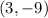`(3,-9)`. And equation of perpendicular line is
`x+y=6`

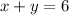
First, we will slope of line
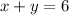`x+y=6`. Let us call it
`m_1`.

`x+y=6\\y=-x+6\\y=mx+c`

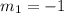`m_1=-1`, that is slope of line
`x+y=6`.

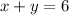Let us call slope of line perpendicular to x+y=6 is
`m_2` .

We know,

`m_1* m_2=-1\\m_2=(-1)/(m_1)`

`m_2=(-1)/(-1)=1`

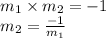
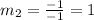
So, the slope of line perpendicular to
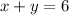`x+y=6` is
`1`

Also, the line passes through point
`(3,-9)`

`(y-y_1)=m(x-x_1)\\(y-(-9))=1(x-3)\\y+9=x-3\\y=x-3-9\\y=x-12\\x-y=12`

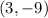
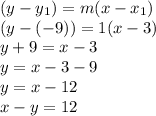
So, the equation for the line in the form of
`ax+by=c` is
`x-y=12`