Question

If 78.2 grams of carbonic acid are sealed in a 2.00 L soda bottle at room temperature (298 K) and decompose completely via the equation below, what would be the final pressure of carbon dioxide assuming it had the full 2.00 L in which to expand? H₂CO₃(aq) → H₂O(l) + CO₂(g)

Answer 1

Answer: The final pressure of carbon dioxide is 15.4 atm

Step-by-step explanation:

To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

• For carbonic acid:

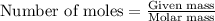
Given mass of carbonic acid = 78.2 g

Molar mass of carbonic acid = 62 g/mol

Putting values in above equation, we get:

`\text{Moles of carbonic acid}=(78.2g)/(62g/mol)=1.26mol`

For the given chemical reaction:

`H_2CO_3(aq.)\rightarrow H_2O(l)+CO_2(g)`

By Stoichiometry of the reaction:

1 mole of carbonic acid produces 1 mole of carbon dioxide

So, 1.26 moles of carbonic acid will produce =
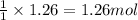`(1)/(1)* 1.26=1.26mol` of carbon dioxide

To calculate the pressure, we use the equation given by ideal gas, which follows:

`PV=nRT`

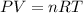
where,

P = pressure of the carbon dioxide = ?

V = Volume of the container = 2.00 L

T = Temperature of the container = 298 K

R = Gas constant =
`0.0821\text{ L. atm }mol^(-1)K^(-1)`

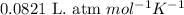
n = number of moles of carbon dioxide = 1.26 moles

Putting values in above equation, we get:

`P* 2.00L=1.26mol* 0.0821\text{ L atm }mol^(-1)K^(-1)* 298K\\\\P=(1.26* 0.0821* 298)/(2.00)=15.4atm`

Hence, the final pressure of carbon dioxide is 15.4 atm