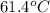Answer : The final temperature of the mixture is
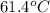
Explanation :
In this problem we assumed that heat given by the hot body is equal to the heat taken by the cold body.
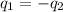
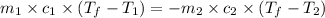
And as we know that,
Mass = Density × Volume
Thus, the formula becomes,
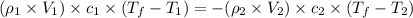
where,
 =
=
 = specific heat of water = same
= specific heat of water = same
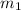 =
=
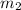 = mass of water = same
= mass of water = same
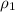 =
=
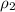 = density of water = 1.0 g/mL
= density of water = 1.0 g/mL
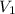 = volume of water at
= volume of water at
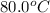 =
=
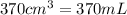
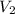 = volume of water at
= volume of water at
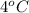 =
=
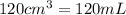
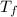 = final temperature of mixture = ?
= final temperature of mixture = ?
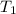 = initial temperature of water =
= initial temperature of water =
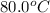
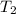 = initial temperature of water =
= initial temperature of water =
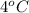
Now put all the given values in the above formula, we get:
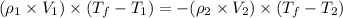
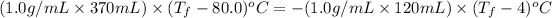
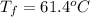
Therefore, the final temperature of the mixture is