Answer:
(a). The volume of the atom is
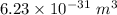
(b). The volume of the nucleus is
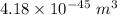
(c). The percentage of the volume of the atom that is occupied by the nucleus is

Step-by-step explanation:
Given that,
Radius of nucleus
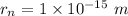
Radius of atom
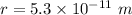
(a). We need to calculate the volume of the atom
Using formula of volume of the atom
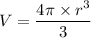
Where, r = radius of atom
Put the value into the formula
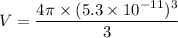

(b). We need to calculate the volume of the nucleus
Using formula of volume of the nucleus
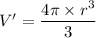
Where, r = radius of atom
Put the value into the formula
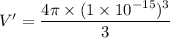
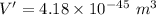
(c). We need to calculate the percentage of the volume of the atom that is occupied by the nucleus
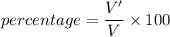
Put the value into the formula
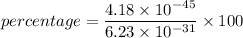
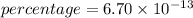
Hence, (a). The volume of the atom is
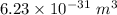
(b). The volume of the nucleus is
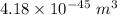
(c). The percentage of the volume of the atom that is occupied by the nucleus is
