Question

The electric field strength 3.5 cm from the surface of a 10-cm-diameter metal ball is 70,000 N/C.What is the charge (in nC) on the ball?

Answer 1

To develop this problem, we will apply the concepts related to the Indian electric field from Coulomb's law. According to the values given we have to the electric field is

`E = 70000N/C`

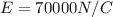
Distance from the center of the ball to the point of consideration is

`r = (10)/(2)+3.5`

`r = 8.5cm`

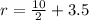
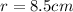
Now the electric field strength is

`E = (kq)/(r^2)`

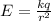
Here,

k = Coulomb's Constant

q = Charge

r = Distance

Rearrange to find the charge,

`q = (Er^2)/(k)`

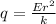
Replacing,

`q = ((70000)(8.5*10^(-2))^2)/(9*10^9)`

`q = 5.6194*10^(-8)`

`q = 56.194nC`

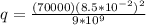
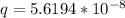
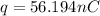
Therefore the charge on the ball is 56.194nC