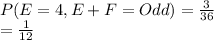Answer:
(a)
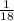 (d)
(d)
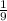
(b)
 (e)
(e)

(c)
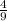 (f)
(f)
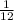
Explanation:
On tossing a 6-face die twice the outcomes of E and F are:
{1, 2, 3, 4, 5 and 6}
And there are total 36 outcomes of the form (E, F).
(a)
The sample space of getting a sum of 11 is: {(5, 6) and (6, 5)}
The probability of getting a sum of 11 is:
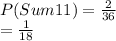
(b)
The sample space of getting an even sum is:
{(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6) (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (4, 6) (5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6)}
The probability of getting an even sum is:
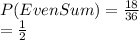
(c)
The sample space of getting an odd sum more than 3 is:
{(1, 4), (1, 6), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4, 1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3) and (6, 5)}
The probability of getting an odd sum more than 3 is:
P (Odd Sum more than 3) =
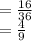
(d)
The sample space of (E, F) such that E is even and less than 6, and F is odd and greater than 1 is:
{(2, 3), (2, 5), (4, 3) and (4, 5)}
The probability such that E is even and less than 6, and F is odd and greater than 1 is:
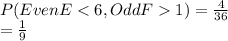
(e)
The sample space of E and F such that E is more than 2, and F is less than 4 is:
E = {3, 4, 5 and 6} F = {1, 2 and 3}
Then the total outcomes of (E, F) will be 12.
The probability such that E is more than 2, and F is less than 4 is:
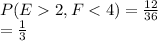
(f)
The sample space of (E, F) such that E is 4 and sum of E and F is odd is:
{(4, 1), (4, 3) and (4, 5)}
The probability such that E is 4 and sum of E and F is odd is: