Question

The production of heat by metabolic processes takes place throughout the volume of an animal, but loss of heat takes place only at the surface (i.e. the skin). Since heat loss must be balanced by heat production if an animal is to maintain a constant internal temperature, the relationship between surface area and volume is relevant for physiology.

If the surface area of a cube is increased by a factor of 2, by what factor does the volume of the cube change? Give your answer to two significant figures. 1.59

Answer 1

To solve this problem we will apply the concepts related to the change in length in proportion to the area and volume. We will define the states of the lengths in their final and initial state and later with the given relationship, we will extrapolate these measures to the area and volume

The initial measures,

`\text{Initial Length} = L`

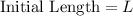
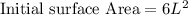`\text{Initial surface Area} = 6L^2` (Surface of a Cube)

`\text{Initial Volume} = L^3`

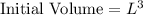
The final measures

`\text{Final Length} = L_f`

`\text{Final surface area} = 6L_f^2`

`\text{Final Volume} = L_f^3`

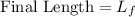
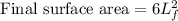
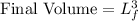
Given,

`((SA)_f)/((SA)_i) = 2`

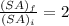
Now applying the same relation we have that

`((L_f)/(L_i))^2 = 2`

`(L_f)/(L_i) = √(2)`

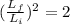
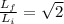
The relation with volume would be

`((Volume)_f)/((Volume)_i) = ((L_f)/(L_i))^3`

`((Volume)_f)/((Volume)_i) = (√(2))^3`

`((Volume)_f)/((Volume)_i) = (2√(2))`

`((Volume)_f)/((Volume)_i) = 2.83`

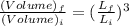
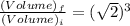
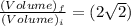
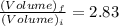
Volume of the cube change by a factor of 2.83