Question

Calculate the mass of oxygen (in mg) dissolved in a 3.14 L bucket of water exposed to a pressure of 1.02 atm of air. Assume the mole fraction of oxygen in air to be 0.21 and the Henry's law constant for oxygen in water at this temperature to be 1.4 × 10-3 M/atm O2. (Enter your value using three significant figures.)

Answer 1

To solve this problem we will apply Henry's law. This law states that at a constant temperature, the amount of gas dissolved in a liquid is directly proportional to the partial pressure exerted by that gas on the liquid. Mathematically it is formulated as follows:

`C_(i) =p_(i)k_{\mathrm {H} }`

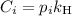
Here

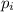`p_(i)` is the partial pressure of the gas.

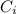`C_(i)` is the concentration of the gas (solubility).

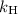`k_{\mathrm {H} }` is Henry's constant, which depends on the nature of the gas, the temperature and the liquid.

At the same time we know the the concentration can be defined as the relation between the number of moles and volume, then

`C_i = \frac{\text{No. Moles}}{V}`

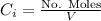
Then we have that the relation can be written now as,

`( \frac{\text{No. Moles}}{V} )= p_(i)k_{\mathrm {H} }`

`\text{No. Moles} =P_i k_{\mathrm {H}} V`

`\text{No. Moles} =(1.02 atm)(3.14L)(1.4*10^(-3)Mol/atm)`

`\text{No. Moles} =4.484mMol`

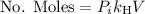
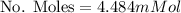
Now the fraction of Oxygen in that quantity is 0.21, then

`\text{No. Moles} = 4.484 * 0.21`

`\text{No. Moles} = 0.94164mMol`

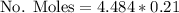
Mass of oxygen

`m = (\text{No. Moles})* (\text{Molecular mass})`

`m = 0.94164mMol * (32(mg)/(mmol))`

`m = 30.1324mg`

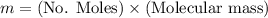
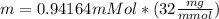
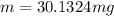
Therefore the mass of oxygen is 30.1324mg