To solve this problem we will apply the concepts related to the electric field. This definition is based on the proposal by Coulomb and will be described in its two states. Under this relationship we will obtain the radius of the distances depending on the elective field.
The electric field strength of the charge from a distance
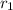 is,
is,
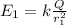
The electric field strength of the charge from a distance
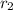 is,
is,
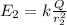
The relation between the electric field strengths
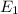 and
and
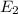 is
is
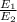 and can be written as
and can be written as

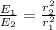

Replacing we have,

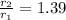
The ratio of the distances
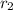 and
and
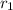 is 1.39
is 1.39