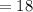Question

Question 13 options:

A jar contains 50 coins, all of which are dimes and quarters.

The total value of the coins in the jar is $7.70.

How many dimes/quarters are in the jar?

Answer 1

The jar has 32 dimes and 18 quarters

Explanation:

To solve this problem we can create a system of linear equations in terms of two-variables (say
`x` and
`y`) and solve it. To begin let us analyze the problem further. We know that the values of each coin type are:

Dimes (
`x` ) = $0.10

Quarters(
`y` ) = $0.25

Total Value = $7.70

Total Coins = 50

Now let us set up our system of equations as:

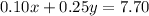`0.10x+0.25y=7.70` Eqn.(1)

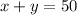`x+y=50` Eqn.(2)

Lets take Eqn.(2) and rerrange it to solve for
`x` as:

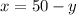`x=50-y` Eqn.(3)

Now lets plug this, in Eqn.(1) so we get the value of
`y` as:

`0.10(50-y)+0.25y=7.70\\\\5-0.10y+0.25y=7.70\\\\-0.10y+0.25y=7.70-5\\\\0.15y=2.7\\\\`

`y=(2.70)/(0.15) \\\\y=18`

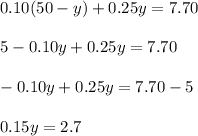
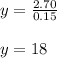
Plugging in
`y=18` back in Eqn.(3) we finally have:

`x=50-18\\x=32`

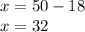
Thus we conclude that in the jar the coins are:

Dimes (
`x` )
`=32`

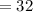
Quarters(
`y` )
`=18`