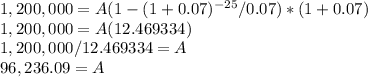Question

Your uncle has $1,200,000 and wants to retire. He expects to live for another 25 years, and he also expects to earn 7% on his invested funds. How much could he withdraw at the beginning of each of the next 25 years and end up with zero in the account? a. $84,703.56 b. $82,162.46 c. $96,236.09 d. $105,032.42 e. $77,080.24

Answer 1

C) $96,236.09

Step-by-step explanation:

To solve this problem, we will use the Present Value of an annuity due formula. The annuity is due because the withdrawals are made at the beginning of each period.

The formula is:

`P = A (1-(1+i)^(-n) / i)*(1+i)`

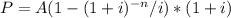
Where:

P = Present value of the annuity

A = Value of each annuity payment

i = Interest rate

n = number of periods

Now, we simply plug the amounts into the formula:

`1,200,000 = A (1-(1+0.07)^(-25) /0.07)*(1+0.07)\\1,200,000 = A (12.469334)\\1,200,000/12.469334 = A\\96,236.09 = A`