Question

Tamara and Jason work at a widget factory. Tamara arrived at work before Jason and began making widgets. Tamara had already made 20 widgets when Jason began his work. Tamara was producing widgets at a rate of 8 widgets per hour. Jason was able to produce widgets at a rate of 12 widgets per hour. At some point, Tamara and Jason will have produced the same number of widgets.

Answer 1

See explanation!

Explanation:

The remaining question reads:

Part A: Write a system of equations to represent the situation. Let x = hours and y = widgets.

Part B: How much time does it take for Tamara and Jason to produce the same number of widgets?

Part C: How many widgets will Tamara and Jason have produced?

-------------------------------------------------------------------------------------------------------------

To solve this problem we can construct an linear algebraic expression for each person, principally denoted as:

`y=ax+c`

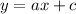
where

`y` :is our dependent variable (which is a function of
`x`)

`x` :is our independent variable

`a` :is the slope

`c` :is the y-intercept constant value (if any present)

Part A: Write a system of equations to represent the situation. Let x = hours and y = widgets.

Tamara

Has already made 20 widgets and produces at a rate of 8 widgets per hour thus here
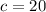`c=20` and
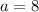`a=8`, so Tamara's equation reads:

`y_(T)=8x+20`

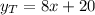
Jason

Has not produced any widgets yet and produces at a rate of 12 widgets per hour thus here
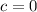`c=0` and
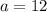`a=12`, so Jason's equation reads:

`y_(J)=12x`

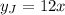
So the system of equations will be

`y_(T)=8x+20\\y_(J)=12x`

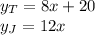
Part B: How much time does it take for Tamara and Jason to produce the same number of widgets?

Since we want to find the amount of time (i.e. the value of
`x` ) it takes for both of them to produce the same number of widgets we can just equate the two equations ans solve for
`x` as follow:

`y_(T)=y_(J)\\8x+20=12x\\8x-12x=-20\\-4x=-20\\x=(-20)/(-4)\\ x=5`

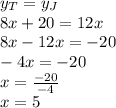
So it takes them 5 hours to produce the same amount of widgets.

Part C: How many widgets will Tamara and Jason have produced?

Now we can simply plug in the value of
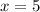`x=5` in any of the two equations (i.e. either for Tamara or Jason) to find the number of widgets produced.

`y_(T)=8(5)+20=40+20=60`

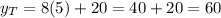
So in a time-space of 5 hours Each will have produced 60 widgets and in total will be 60+60 = 120 widgets.