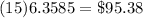You have to make 1000 buttons.the diameter of the button is 9cm but you have to find it’s area.its $15/m squared and you have to find how much it costs to make 1000 buttons.

Question

asked Jul 19, 2021 3.4k views

1 Answer

Iuriimoz · Answer 1 · 2021-07-23T16:40:51+0000

Answer:

$95.38

Explanation:

step 1

Find the area of one button

The area is equal to

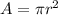
$A=\pi r^(2)$

we have

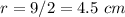$r=9/2=4.5\ cm$ ---> the radius is half the diameter

Convert to meters

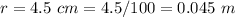
$r=4.5\ cm=4.5/100=0.045\ m$

assume

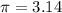
$\pi =3.14$

substitute

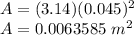
$A=(3.14)(0.045)^(2)\\A=0.0063585\ m^2$

step 2

Find the area of 1,00 buttons

Multiply by 1,000

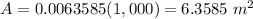
$A=0.0063585(1,000)=6.3585\ m^2$

step 3

Find the cost

Multiply $15 per square meter by the total area of 1,000 buttons

$(15)6.3585=\$95.38$