Question

Pls help, every time I do this problem I get a graph that doesn’t match any of these

Answer 1

2nd choice (see below)

Explanation:

The base of the logarithm is 1/5, so the logs of larger numbers will be more and more negative. 3 is subtracted from the logarithm.

A couple of points on the curve are ...

`f(1)=\log_{(1)/(5)}{(1)}-3=0-3=-3 \qquad\text{point (1,-3)}`

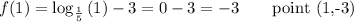
This point is on curves B and D.

Another point is ...

`f(5)=\log_{(1)/(5)}{(5)}-3=-1-3=-4 \qquad\text{point (5,-4)}`

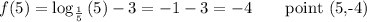
This point is on curve B.

_____

If your graphing calculator cannot handle fractional bases, you can use the change of base formula to rewrite the function as ...

f(x) = log(x)/log(1/5) -3 ≈ -1.43067656·log(x) -3

Note that the multiplier is negative, so the function value will head toward +∞ as x→0.