Step-by-step explanation:
When Michelson-Morley apparatus is turned through
 then position of two mirrors will be changed. The resultant path difference will be as follows.
then position of two mirrors will be changed. The resultant path difference will be as follows.
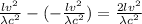
Formula for change in fringe shift is as follows.
n =

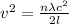
v =
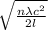
According to the given data change in fringe is n = 1. The data is Michelson and Morley experiment is as follows.
l = 11 m
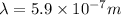
c =
 m/s
m/s
Hence, putting the given values into the above formula as follows.
v =
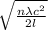
=
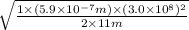
=

Thus, we can conclude that velocity deduced is
 .
.