Answer:
The final temperature is 64.28°C.
Step-by-step explanation:
Imagine now that one tried to repeat the same measurement, but between the time that the 400 cm³ of warm water was measured at 88°C and the time it was mixed with the 130 cm³ of cooler water at 15°C, the warmer water had lost 3060 cal to the environment. Calculate the final equilibrium temperature assuming no heat loss after mixing occurs.
Let the temperature of hot water before mixing is t
We need to calculate the temperature
Using formula of energy
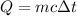
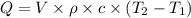
Put the value into the formula

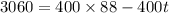
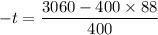
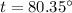
We need to calculate the final temperature
Using formula of temperature
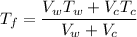
Put the value into the formula

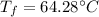
Hence, The final temperature is 64.28°C.