Question

The royal fruit company produces two types of fruit drinks. The first type is 20% pure fruit juice and the second type is 45% pure fruit juice. The company is attempting to produce a fruit drink that contains 40% pure fruit juice. How many pints of each of the two existing types of drink must be used to make 30 pints of a mixture that is 40% pure fruit juice?

Answer 1

6 pints of 20% pure fruit juice and 24 pints of 45 % pure fruit juice is mixed to get 30 pints of mixture of 40 % pure fruit juice

Solution:

The final volume is 30 pints of mixture of 40 % pure fruit juice

Let "x" be the volume of 20 % pure fruit juice

Then, (30 - x) is the volume of 45 % pure fruit juice

Then, we can say,

"x" be the volume of 20 % pure fruit juice and (30 - x) is the volume of 45 % pure fruit juice is mixed to get 30 pints of mixture of 40 % pure fruit juice

Therefore, we frame a equation as:

`x * 20 \% + (30-x) * 45 \% = 30 * 40 \%`

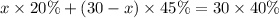
Solve the above expression for "x"

`x * (20)/(100) + (30-x) * (45)/(100) = 30 * (40)/(100)\\\\0.2x+0.45(30-x) = 12\\\\0.2x + 13.5 - 0.45x = 12\\\\\text{Keep the variables in left side of equation and move constants to other side }\\\\0.2x - 0.45x = 12 - 13.5\\\\-0.25x = -1.5\\\\0.25x = 1.5\\\\\text{Divide both sides of equation by 0.25}\\\\x = 6`

So, 6 pints of 20% pure fruit juice

Then, (30 - x) = 30 - 6 = 24

24 pints of 45 % pure fruit juice is used