Question

When 258 college students are randomly selected and surveyed, it is found that 106 own a car. Find a 99% confidence interval for the true proportion of all college students who own a car. 0.351 < p < 0.471 0.332 < p < 0.490 0.339 < p < 0.482 0.360 < p < 0.461

Answer 1

Answer: 0.332 < p < 0.490

Explanation:

We know that the confidence interval for population proportion is given by :-

`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

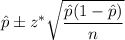
, where n= sample size

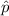`\hat{p}` = sample proportion

z* = critical z-value.

As per given , we have

n= 258

Sample proportion of college students who own a car =
`\hat{p}=(106)/(258)\approx0.411`

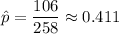
Critical z-value for 99% confidence interval is 2.576. (By z-table)

Therefore , the 99% confidence interval for the true proportion(p) of all college students who own a car will be :
`0.411\pm (2.576)\sqrt{(0.411(1-0.411))/(258)}\\\\=0.411\pm (2.576)√(0.00093829)\\\\= 0.411\pm (2.576)(0.0306315197142)\\\\=0.411\pm 0.0789=(0.411-0.0789,\ 0.411+0.0789)\\\\=(0.3321,\ 0.4899)\approx(0.332,\ 0.490)`

Hence, a 99% confidence interval for the true proportion of all college students who own a car : 0.332 < p < 0.490