Answer:
The speed of plane is
 , and speed wind is
, and speed wind is
 .
.
Explanation:
Given against the wind the airline flew
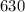 miles in
miles in
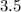 hours.
hours.
including the tailwind the return trip took
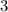 hours.
hours.
Let speed of plane is
 .
.
Also, speed of the wind is
 .
.
Now, we will find speed on each case.
Speed against the wind is

Speed with the wind is
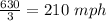
Now, we will write the equation
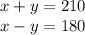
Add these equation we get,
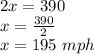
Now, plug this value in
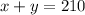 to get speed of wind
to get speed of wind
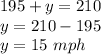
So, the speed of plane in still air is
 , and speed of the wind is
, and speed of the wind is
 .
.