Answer:
(a). The change in the kinetic energy of his center of mass during this process is -495 J.
(b). The average force is 1650 N.
Step-by-step explanation:
Given that,
Mass = 110 kg
Speed = 3.0 m/s
Distance = 30 cm
(a). We need to calculate the change in the kinetic energy of his center of mass during this process
Using formula of kinetic energy
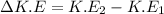
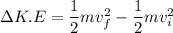
Put the value into the formula
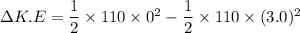
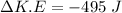
(b). We need to calculate the average force must he exert on the railing
Using work energy theorem
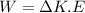
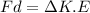

Put the value into the formula
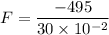
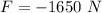
The average force is 1650 N.
Hence, (a). The change in the kinetic energy of his center of mass during this process is -495 J.
(b). The average force is 1650 N.