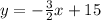Question

P (6,6) y=2/3x

i need a equation of the line perpendicular to the given line that contains P ( can anybody answer the full problem (showing work for 35 points) ??

Answer 1

`y = -(3)/(2)x+15`

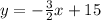
Explanation:

Given:

Given point P(6, 6)

The equation of the line.

`y = (2)/(3)x`

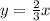
We need to find the equation of the line perpendicular to the given line that contains P

Solution:

The equation of the line.

`y = (2)/(3)x`

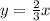
Now, we compare the given equation by standard form
`y = mx +c`

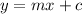
So, slope of the line
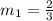`m_(1) = (2)/(3)`, and

y-intercept
`c=0`

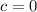
We know that the slope of the perpendicular line
`m_(1)* m_(2) = -1`

`m_(2)=-(1)/(m_(1))`

`m_(2)=-(1)/((2)/(3) )`

`m_(2)=-(3)/(2)`

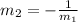
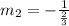
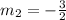
So, the slope of the perpendicular line
`m_(2)=-(3)/(2)`

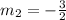
From the above statement, line passes through the point P(6, 6).

Using slope intercept formula to know y-intercept.

`y=mx+c`

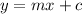
Substitute point
`P(x_(1), y_(1))=P(6, 6)` and
`m = m_(2)=-(3)/(2)`

`6=-(3)/(2)* 6 +c`

`6=-3* 3 +c`

`c=6+9`

`c=15`

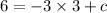
So, the y-intercept of the perpendicular line
`c=15`

Using point slope formula.

`y=mx+c`

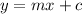
Substitute
`m = m_(2)=-(3)/(2)` and
`c=15` in above equation.

`y = -(3)/(2)x+15`

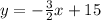
Therefore: the equation of the perpendicular line
`y = -(3)/(2)x+15`