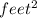Question

You are giving 24 linear feet of fencing all 3 feet tall you wish to make the largest rectangular enclosure possible to maximize space what should the dimensions of the enclosure be

Answer 1

The largest area enclosed is A = xy = 6 feet
`*` 6 feet = 36
`feet^(2)`

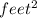
Explanation:

i) The perimeter of the area is 2
`*`(x + y) =24 ∴ x + y = 12 ∴ y = 12 - x

ii) The area of rectangle enclosed A = xy ⇒ A = x ( 12 - x) = 12x -
`x^(2)`

iii) differentiating both sides of the equation in ii) we get

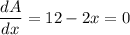`(dA)/(dx) = 12 - 2x = 0` ⇒ x = 6 feet

iv) Differentiating both sides of equation in iii) we get
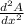`(d^(2)A)/(dx^(2) )` = -2

Therefore the area enclosed is maximum as the double derivative is negative

v) therefore for largest area enclosed x = 6 feet and y = 12 - 6 = 6 feet

vi) therefore the largest area enclosed is

A = xy = 6 feet
`*` 6 feet = 36
`feet^(2)`