Question

What is the similarity ratio of ΔABC to ΔDEF?
Tri ABC: AC=4 CB=5
Tri DEF: DF= 2

Answer 1

The similarity ratio of ΔABC to ΔDEF = 2 : 1.

Solution:

The image attached below.

Given ΔABC to ΔDEF are similar.

To find the ratio of similarity triangle ABC and triangle DEF.

In ΔABC: AC = 4 and CB = 5

In ΔDEF: DF = 2, EF = ?

Let us first find the length of EF.

We know that, If two triangles are similar, then the corresponding sides are proportional.

⇒
`(AC)/(DF) =(BC)/(EF)`

⇒
`(4)/(2) =(5)/(EF)`

⇒
`4EF=5*2`

⇒
`EF=(5* 2)/(4)`

⇒
`EF=(5)/(2)`

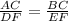
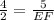
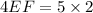
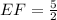
Ratio of ΔABC to ΔDEF =
`(AC)/(DF) =(4)/(2)=(2)/(1)`

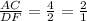
Similarly, ratio of ΔABC to ΔDEF =
`(BC)/(EF) =(5)/((5)/(2))=(2)/(1)`

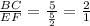
Hence, the similarity ratio of ΔABC to ΔDEF = 2 : 1.