Question

The position of a particle is given by the expression x 5 4.00 cos (3.00pt 1 p), where x is in meters and t is in seconds. Determine

(a) the frequency
(b) period of the motion
(c) the amplitude of the motion
(d) the phase constant
(e) the position of the particle at t 5 0.250 s.

Answer 1

1.5 Hz

0.67 s

4 m

`\pi`

2.82842 m

Step-by-step explanation:

The equation is

`x=4cos(3\pi t+\pi)`

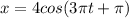
It is of the form

`x=Acos(2\pi ft+\phi)`

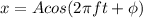
Comparing the equations we get

`3\pi=2\pi f\\\Rightarrow f=(3)/(2)\\\Rightarrow f=1.5\ Hz`

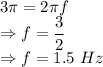
Frequency is 1.5 Hz

Time period is given by

`T=(1)/(f)\\\Rightarrow T=(1)/(1.5)\\\Rightarrow T=0.67\ s`

The period of the motion is 0.67 s

Amplitude

`A=4\ m`

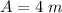
Amplitude is 4 m

Phase constant

`\phi=\pi`

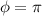
The phase constant is
`\pi`

At t = 0.25 s

`x=4cos(3\pi t+\pi)\\\Rightarrow x=4cos(3\pi* 0.25+\pi)\\\Rightarrow x=2.82842\ m`

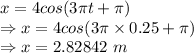
The position of the particle is 2.82842 m