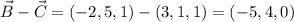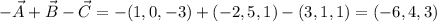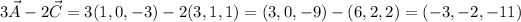Answer:
The calculated vectors are:
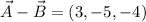
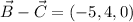
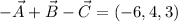
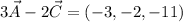
Step-by-step explanation:
To operate with vectors, you sum or rest component to component. To multiply scalars with vectors, you distribute the scalar with each component of the vector. These are the following rules you must apply in these cases:
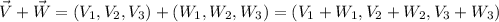 (1)
(1)
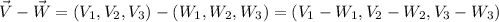 (2)
(2)
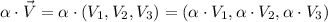 (3)
(3)
The operations in these cases are: