Question

Keith drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 8 hours. When Keith drove home, there was no traffic and the trip only took 5 hours. If his average rate was 21 miles per hour faster on the trip home, how far away does Keith live from the mountains? Do not do any rounding.

Answer 1

Keith live 280 miles far way from the mountains.

Explanation:

Consider the provided information.

Keith drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 8 hours.

Let the distance is D and average rate or speed is x miles.

`Distance =Speed* Time`

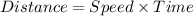
Substitute the respective values.

`D=x* 8\\D=8x`

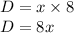
When Keith drove home, there was no traffic and the trip only took 5

hours. The average rate was 21 miles per hour faster on the trip home,

The average rate or speed during return is x+21 miles.

Substitute the respective values in the above formula.

`D =(x+21)* 5\\D=5x+105`

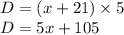
Equate both the equations.

`5x+105=8x\\3x=105\\x=35`

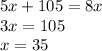
Substitute the value of x in
`D=8x`

`D=8(35)\\D=280`

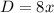
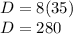
Hence, Keith live 280 miles far way from the mountains.