Answer:
The average life of the mice that are placed on this diet is less than 40 months.
Explanation:
Consider the provided information.
When 40% of the calories in their diet are replaced by vitamins and protein. Is there any reason to believe that μ < 40.
The null and alternative hypothesis are:
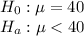
64 mice that are placed on this diet have an average life is 38 months with a standard deviation of 5.8 months.
Therefore,
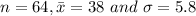
Use the formula:
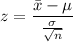
Substitute the respective values in the above formula.

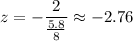
Now using the table
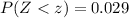
The p value is smaller than 0.05 so reject the null hypothesis.
Therefore, the average life of the mice that are placed on this diet is less than 40 months.