Question

a packe of cards conatins 4 red and 5 black cards. a hand of 5 cards is drawn without replacment. What is the proablity of all five black. of exactly three black?

Answer 1

Answer: Our required probability is 0.3387.

Explanation:

Since we have given that

Number of red cards = 4

Number of black cards = 5

Number of cards drawn = 5

We need to find the probability of getting exactly three black cards.

Probability of getting a black card =
`(5)/(9)`

Probability of getting a red card =
`(4)/(9)`

So, using "Binomial distribution", let X be the number of black cards:

`P(X=3)=^5C_3((5)/(9))^3((4)/(9))^2\\\\P(X=3)=0.3387`

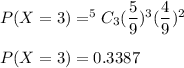
Hence, our required probability is 0.3387.