The diameter of hemisphere is 61.4 units
Solution:
Given that, volume of hemisphere is 60570 cubic units
To find: Diameter of hemisphere
The formula for volume of hemisphere is given as:
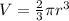
Where, "r" is the radius of hemisphere
Substituting the values we get,
![60570 = (2)/(3) * 3.14 * r^3\\\\60570 = 2.093 * r^3\\\\r^3 = (60570)/(2.093)\\\\r^3 = 28939.32\\\\\text{Take cube root on both sides }\\\\r = \sqrt[3]{28939.32} \\\\r = 30.7017248 \approx 30.7](https://img.qammunity.org/2021/formulas/mathematics/middle-school/neh9etvr8oay6k3n4omkm900jwfx96isus.png)
We know diameter is twice of radius
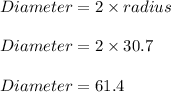
Thus diameter of hemisphere is 61.4 units