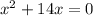Question

What are the quadratic equations for x=-14​

Answer 1

`x^(2) +14x=0`

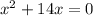
Explanation:

Given:

Given root is

`x=-14,\ 0`

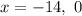
Now we need to find the quadratic equation for given roots.

Solution:

The given roots are -14 and 0.

So, the sum of the roots.

`\alpha +\beta = -14 + 0`

`\alpha +\beta = -14`

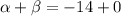
Product of the given roots

`\alpha* \beta = -14* 0`

`\alpha* \beta = 0`

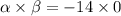
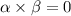
Therefore, the required quadratic equation is.

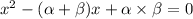`x^(2) -(\alpha +\beta )x+\alpha* \beta=0` -------------------(1)

Now we substitute
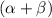`(\alpha +\beta )` and
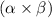`(\alpha* \beta)` in equation 1.

`x^(2) -(-14)x+0=0`

`x^(2) +14x=0`

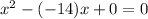
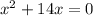
Therefore, the quadratic equation for the given root is.
`x^(2) +14x=0`