Question

A 1100 kg car rounds a curve of radius 68 m banked at an angle of 16 degrees. If the car is traveling at 95 km/h, will a friction force be required? If so, how much and in what direction?

Answer 1

Determining if a friction force is required for a car rounding a banked curve depends on the car's speed relative to the curve's ideal speed. At 95 km/h, a frictional force may be needed if this speed is not the ideal speed for the 68 m radius curve banked at 16 degrees.

Step-by-step explanation:

When a 1100 kg car rounds a curve of radius 68 m banked at an angle of 16 degrees, we need to determine if a friction force is required when the car is traveling at 95 km/h. If the car is traveling at the correct banked curve speed, it could complete the turn without any frictional force. However, if the car travels at a speed higher or lower than this optimal speed, a frictional force will be necessary either to prevent the car from slipping outward or to prevent it from falling inward towards the center of the curve.

To find out whether a friction force is needed, we first need to calculate the ideal speed for this banked turn. This involves calculating the speed at which the components of the normal force provide enough centripetal force for the turn. The ideal speed is reached when no friction force is needed to keep the car on the path, meaning the force of gravity, the normal force, and the centripetal force are in perfect balance.

However, if the car is indeed traveling at 95 km/h, faster or slower than this ideal speed, then either a static frictional force acting upwards along the bank or a static frictional force opposite to the car's direction would be required to maintain its circular path without slipping.

Answer 2

Yes. Towards the center. 8210 N.

Step-by-step explanation:

Let's first investigate the free-body diagram of the car. The weight of the car has two components: x-direction: towards the center of the curve and y-direction: towards the ground. Note that the ground is not perpendicular to the surface of the Earth is inclined 16 degrees.

In order to find whether the car slides off the road, we should use Newton's Second Law in the direction of x: F = ma.

The net force is equal to
`F = (mv^2)/(R) = (1100* (26.3)^2)/(68) = 1.1* 10^4~N`

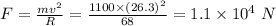
Note that 95 km/h is equal to 26.3 m/s.

This is the centripetal force and equal to the x-component of the applied force.

`F = mg\sin(16) = 1100(9.8)\sin(16) = 2.97*10^3`

As can be seen from above, the two forces are not equal to each other. This means that a friction force is needed towards the center of the curve.

The amount of the friction force should be
`8.21* 10^3~N`

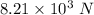
Qualitatively, on a banked curve, a car is thrown off the road if it is moving fast. However, if the road has enough friction, then the car stays on the road and move safely. Since the car intends to slide off the road, then the static friction between the tires and the road must be towards the center in order to keep the car in the road.