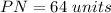Question

If LO = 15x+19 and QN = 10x+2 find PN

Answer 1

`PN=64\ units`

Explanation:

The complete question is

Given the quadrilateral is a rectangle, if LO = 15x+19 and QN = 10x+2 find PN

see the attached figure to better understand the problem

we know that

The diagonals of a rectangle are congruent and bisect each other

so

`QN=(1)/(2)LO`

substitute the given values

`10x+2=(1)/(2)(15x+19)`

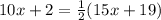
solve for x

`20x+4=15x+19\\20x-15x=19-4\\5x=15\\x=3`

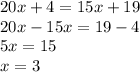
Find the length of PN

Remember that

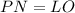`PN=LO` ----> diagonals of rectangle are congruent

`LO=15x+19`

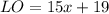
substitute the value of x

`LO=15(3)+19=64\ units`

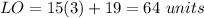
therefore

`PN=64\ units`