Answer: Asteroid 1 has more mass than asteroid 2
Step-by-step explanation:
Let's begin by explaining this crash between both asteroids is known as an elasic collision, since both followed opposite paths after they crashed.
In addition, according to the conservation of momentum law it is stated the following:
"If two objects or bodies are in a closed system and both collide, the total momentum of these two objects before the collision will be the same as the total momentum of these same two objects after the collision".
This means the momentum before the collision (
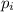 ) is equal to the momentum after the collision (
) is equal to the momentum after the collision (
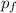 ). Hence the momentum is conserved:
). Hence the momentum is conserved:
 (1)
(1)
Before the crash:
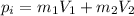 (2)
(2)
Where:
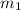 is the mass of the first asteroid
is the mass of the first asteroid
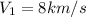 is the velocity of the first asteroid
is the velocity of the first asteroid
 is the mass of the second asteroid
is the mass of the second asteroid
 is the velocity of the second asteroid
is the velocity of the second asteroid
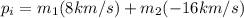 (3)
(3)
After the crash:
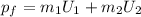 (4)
(4)
Where:
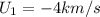 is the final velocity of the first asteroid
is the final velocity of the first asteroid
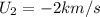 is the final velocity of the second asteroid
is the final velocity of the second asteroid
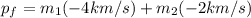 (5)
(5)
Substituting (3) and (5) in (1):
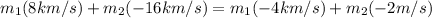 (6)
(6)
Grouping similar terms:
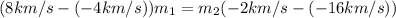 (7)
(7)
Then:
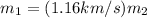 (8) This means
(8) This means
 must be multiplied by 1.16 km/s in order to make this side of the equation equal to
must be multiplied by 1.16 km/s in order to make this side of the equation equal to
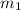 .
.
Hence:
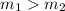
Asteroid 1 has more mass than asteroid 2