Question

A farmhouse shelters 18 animals. Some are cows and some are chickens. Altogether there are 68 legs how many of each animal are there?

Answer 1

The number of cows in farmhouse shelter is 16

The number of chickens in farmhouse shelter is 2 .

Explanation:

Total number of animals in farmhouse shelters = 18

Total number of legs of both animals = 68 legs

Let The number of cows = C

Let The number of chickens = c

∵ the number of legs does each cow has = 4

And, The number of legs does each chicken has = 2

According to question

∵Total number of animals in farmhouse shelters = 18

i.e number of cows + number of chickens = 18

Or, C + c = 18 .....1

Again

∵ Total number of legs of both animals = 68 legs

i.e number of cows × number of legs does each cow has + number of chickens × number of legs does each chicken has = 68

Or, C × 4 + c × 2 = 68

i.e 4 C + 2 c = 68 ........2

Solving eq 1 and eq 2 , we get

(4 C + 2 c ) - 2 × (C + c) = 68 - 2 × 18

Or, (4 C - 2 C) + (2 c - 2 c) = 68 - 36

Or, 2 C + 0 = 32

∴ C =
`(32)/(2)`

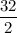
i.e C = 16

So, The number of cows in farmhouse shelter = C = 16

Again

Put the value of C into eq 1

∵ C + c = 18

Or, c = 18 - C

Or, c = 18 - 16

i.e c = 2

So, The number of chickens in farmhouse shelter = c = 2

Hence, The number of cows in farmhouse shelter is 16 and The number of chickens in farmhouse shelter is 2 . Answer