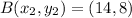Question

M is the midpoint of AB
A(2,14) and M(8,11) Find the coordinates of the missing endpoint.

Answer 1

Therefore, the coordinates of the missing endpoint.is

`B(x_(2),y_(2))=(14,8)`

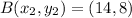
Explanation:

Given:

M is the midpoint of AB

Let ,

A(x₁ , y₁) = (2,14) and

M( x , y ) = (8,11)

To Find:

B(x₂ , y₂) = ?

Solution:

M is the midpoint of AB then By Mid point Formula the Coordinate of M is given by,

`Mid\ point(AB)=((x_(1)+x_(2) )/(2), (y_(1)+y_(2) )/(2))`

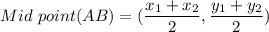
Substituting the values we get

`M(8,11)=((2+x_(2) )/(2), (14+y_(2) )/(2))`

By Equality property we have

`8=(2+x_(2) )/(2)\ and\ 11=(14+y_(2) )/(2)`

`16=2+x_(2)\ and\ 22=14+y_(2)`

`16-2=x_(2)\ and\ 22-14=y_(2)`

`14=x_(2)\ and\ 8=y_(2)`

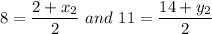
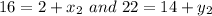
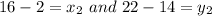
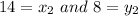
Therefore, the coordinates of the missing endpoint.is

`B(x_(2),y_(2))=(14,8)`