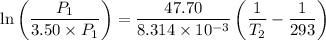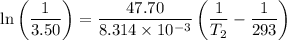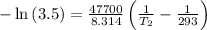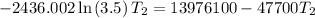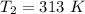Answer:
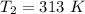
Step-by-step explanation:
he expression for Clausius-Clapeyron Equation is shown below as:
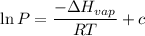
Where,
P is the vapor pressure
ΔHvap is the Enthalpy of Vaporization
R is the gas constant (8.314×10⁻³ kJ /mol K)
c is the constant.
For two situations and phases, the equation becomes:
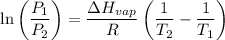
Given:
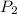 = 3.50
= 3.50
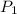
 = 293 K
= 293 K
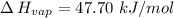
So,