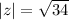Answer:
Explanation:
The absolute value of z is the distance between the point graphed from the complex number and the origin on a complex plane. In a complex plane, the x axis is replaced by R, real numbers, and the y axis is replaced by i, the complex part of the complex number. Our real number is positive 3 and the complex number is -5, so we go to the right 3 and then down 5 and make a point. Connect that point to the origin and then connect the point to the x axis at 3 to construct a right triangle that has a base of 3 and a length of -5. To find the distance of the point to the origin is to find the length of the hypotenuse of that right triangle using Pythagorean's Theorem. Therefore:
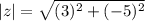 and
and
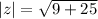 and
and