Question

4. A geometric sequence is defined recursively by a(1) = 40 and a(n)= a(n-1)

(a) Write out the first four terms of this sequence.

(b) Is the 9th term of this sequence larger or smaller than 1/10? Show the calculation that you use to determine your answer.

Answer 1

The complete question is:

A geometric sequence is defined recursively by

`a_((1))=40\text{ and }a_n=(-1/2)a_((n-1))`

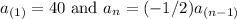
(a) Write out the first four terms of this sequence.

(b) Is the 9th term of this sequence larger or smaller than 1/10? Show the calculation that you use to determine your answer.

Answer:

• The 9th term is larger than 1/10.

Step-by-step explanation:

You are given the first term,
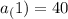`a_(1)=40` , and the recursive formula

`a_((n))=(-1/2)a_((n-1)`

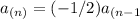
Thus, you can find the sequence of terms by multiplying each term by the constant ratio, (-1/2).

(a) First four terms of the sequence

`a_((1))=40\\ \\ a_((2))=40* (-1/2)=-20\\ \\ a_((3))=-20* (-1/2)=10\\\\ a_((4))=10* (-1/2)=-5`

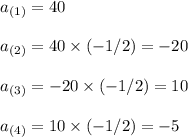
Those are the first four terms.

(b) 9th term

You can write the explicit formula of the sequence as:

`a_((n))=a_((1))* r^((n-1))\\ \\ a_((n))=40(-1/2)^((n-1))`

Thus, for the 9th term, n = 9, and the term is:

`a_((9))=40* (-1/2)^((9-1))\\ \\ a_((9))=40*(-1/2)^8\\ \\ a_((9))=40*(1/256)=0.1526`

Since 1/10 = 0.1, and 0.1 < 0.1526, the 9th term is larger than 1/10.