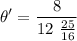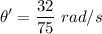Question

A balloon rises at the rate of 8 feet per second from a point on the ground 12 feet from an observer. To 2 decimal places in radians per second, find the rate of change of the angle of elevation when the balloon is 9 feet above the ground.

Answer 1

`\displaystyle \theta' =0.24\ rad/s`

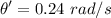
Step-by-step explanation:

Rate Of Change

Let some variable y depend on time t. we can express y as a function of t as

`y=f(t)`

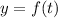
The instant rate of change of y respect to t is the first derivative, i.e.

`y'=f'(t)`

The balloon, the ground and the observer form a right triangle (shown below) where the height of the balloon y, the horizontal distance x, and the angle of elevation are related with the trigonometric formula

`\displaystyle tan\theta =(y)/(x)`

Since x is constant, we take the derivative with respect to time by using the chain rule:

`\displaystyle sec^2\theta \ \theta' =(y')/(x)`

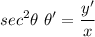
Solving for
`\theta'`

`\displaystyle \theta' =(y')/(xsec^2\theta)`

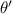
Let's compute the actual angle with the initial conditions y=9 feet, x=12 feet

`\displaystyle tan\theta =(y)/(x)`

`\displaystyle tan\theta =(9)/(12)=(3)/(4)`

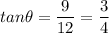
Knowing that

`\sec^2\theta=1+tan^2\theta`

`\displaystyle \sec^2\theta=1+\left((3)/(4)\right)^2`

`\displaystyle \sec^2\theta=(25)/(16)`

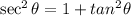
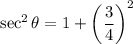
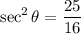
The balloon is rising at y'=8 feet/sec, thus we compute the change of the angle of elevation:

`\displaystyle \theta' =(8)/(12\ (25)/(16))`

`\displaystyle \theta' =(32)/(75)\ rad/s`

`\boxed{\displaystyle \theta' =0.43\ rad/s}`