Answer:
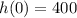
The above function value for
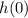 shows that height of the ball before it was dropped i.e. at time = 0 seconds.
shows that height of the ball before it was dropped i.e. at time = 0 seconds.
The height of the ball above the ground before it was dropped = 400 ft.
Explanation:
Given:
The quadratic function that models the height of the baseball above the ground in feet ,
 seconds after it was dropped is given as:
seconds after it was dropped is given as:
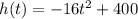
To find
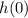 and interpret the meaning of the function value in contect of the problem.
and interpret the meaning of the function value in contect of the problem.
Solution:
In order to find
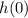 , we will replace
, we will replace
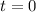 in the given function as
in the given function as
 is a function of time
is a function of time
 .
.
Thus, we have:
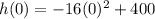
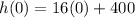
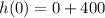
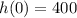 (Answer)
(Answer)
The above function value for
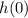 shows that height of the ball before it was dropped i.e. at time = 0 seconds.
shows that height of the ball before it was dropped i.e. at time = 0 seconds.
The height of the ball above the ground before it was dropped = 400 ft.