Question

Find the tangent line approximation for 10+x−−−−−√ near x=0. Do not approximate any of the values in your formula when entering your answer below.

Answer 1

`L(x)=√(10)+(√(10))/(20)x`

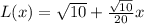
Explanation:

We are asked to find the tangent line approximation for
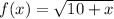`f(x)=√(10+x)` near
`x=0`.

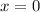We will use linear approximation formula for a tangent line
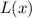`L(x)` of a function
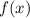`f(x)` at
`x=a` to solve our given problem.

`L(x)=f(a)+f'(a)(x-a)`

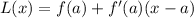
Let us find value of function at
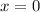`x=0` as:

`f(0)=√(10+x)=√(10+0)=√(10)`

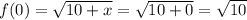
Now, we will find derivative of given function as:

`f(x)=√(10+x)=(10+x)^{(1)/(2)}`

`f'(x)=(d)/(dx)((10+x)^{(1)/(2)})\cdot (d)/(dx)(10+x)`

`f'(x)=(1)/(2)(10+x)^{-(1)/(2)}\cdot 1`

`f'(x)=(1)/(2√(10+x))`

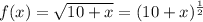
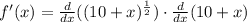
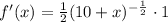
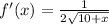
Let us find derivative at
`x=0`

`f'(0)=(1)/(2√(10+0))=(1)/(2√(10))`

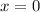
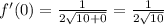
Upon substituting our given values in linear approximation formula, we will get:

`L(x)=√(10)+(1)/(2√(10))(x-0)`

`L(x)=√(10)+(1)/(2√(10))x-0`

`L(x)=√(10)+(√(10))/(20)x`

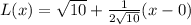
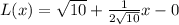
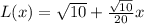
Therefore, our required tangent line for approximation would be
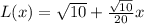`L(x)=√(10)+(√(10))/(20)x`.