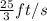Answer:
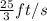
Step-by-step explanation:
Height of man= 6ft
Height of light=1 5ft
Let BC=x and CD=y
BD=x+y
Triangle ABD and ECD are similar
When two triangles are similar then the ratio of their corresponding sides are equal
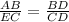
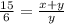
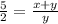
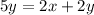

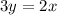
Differentiate w.r.t t

We have
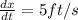
Substitute the value then we get
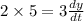
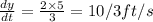
Rate at which the tip of shadow is moving=
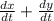
Rate at which the tip of shadow is moving=
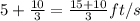
Rate at which the tip of shadow is moving=