Question

∆JKL~∆MNO and J/K MN =2/3 find the length of NO if KL=12.

Answer 1

Therefore the length of NO is 18 units.

Explanation:

Given:

∆JKL~∆MNO and

`(JK)/(MN)=(2)/(3)`

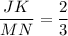
KL = 12.

To Find :

the length of NO = ?

Solution:

Δ JKL ~ Δ LMN ….{Given)

If two triangles are similar then their sides are in proportion.

`(JK)/(MN) =(KL)/(NO)=(JL)/(MO) \textrm{corresponding sides of similar triangles are in proportion}\\`

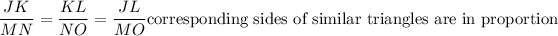
Substituting the values we get

`(2)/(3) =(12)/(NO)\\\\NO=(36)/(2)=18\\\\NO=18\ unit`

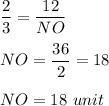
Therefore the length of NO is 18 units.